Sum

Sum là tổng của tất cả các giá trị dữ liệu.


Mean

Sử dụng giá trị trung bình “Mean” để mô tả mẫu với một giá trị duy nhất đại diện cho trung tâm của dữ liệu. Nhiều phân tích thống kê sử dụng giá trị trung bình “Mean” như một thước đo tiêu chuẩn cho trung tâm của sự phân phối dữ liệu.
 

Standard deviation

Sử dụng độ lệch chuẩn “Standard deviation” để xác định mức độ trải rộng của dữ liệu so với giá trị trung bình. Để biết thêm thông tin, hãy tham khảo bài viết: Độ lệch chuẩn là gì?
 

Minimum

Giá trị nhỏ nhất “Minimum” là giá trị dữ liệu nhỏ nhất trong mẫu “Sample”. Sử dụng giá trị tối thiểu “Min” để xác định một lỗi ngoại lệ có thể xảy ra hoặc một lỗi nhập dữ liệu. Một trong những cách đơn giản nhất để đánh giá mức độ lan truyền dữ liệu của bạn là so sánh mức tối thiểu và mức tối đa.


Maximum

Giá trị lớn nhất “Max” là giá trị dữ liệu lớn nhất trong mẫu “Sample”. Sử dụng giá trị tối đa để xác định lỗi ngoại lệ có thể xảy ra hoặc lỗi nhập dữ liệu. Một trong những cách đơn giản nhất để đánh giá mức độ lan truyền dữ liệu của bạn là so sánh mức tối thiểu và mức tối đa.
 

Range

Phạm vi “Range” là sự khác biệt giữa giá trị dữ liệu lớn nhất và nhỏ nhất trong mẫu. Phạm vi đại diện cho khoảng nhỏ nhất chứa tất cả các giá trị dữ liệu.
 

Median

Trung vị “Median” là một thước đo khác về trung tâm của sự phân phối dữ liệu. Giá trị trung vị “Median” thường ít bị ảnh hưởng bởi các giá trị ngoại lai hơn giá trị trung bình “Mean”. Một nửa giá trị dữ liệu lớn hơn giá trị trung vị và một nửa giá trị dữ liệu nhỏ hơn giá trị trung vị.


Sum of squares

Tổng bình phương “Sum of squares” chưa hiệu chỉnh được tính bằng cách bình phương từng giá trị trong cột, sau đó cộng các giá trị bình phương đó. Ví dụ, nếu cột chứa x1, x2, ..., xn, thì tổng bình phương được tính là (x₁² + x₂² + ... + x_n²). Không giống như tổng bình phương được hiệu chỉnh “Corrected sum of squares”, tổng bình phương chưa được hiệu chỉnh bao gồm lỗi. Các giá trị dữ liệu được bình phương mà không trừ giá trị trung bình “Mean” trước.

 
N total

N total là Tổng số quan sát trong cột. Dùng để biểu diễn tổng của N thiếu “N missing” và N không thiếu “N nonmissing”. Minitab hiển thị giá trị này trong đầu ra dưới dạng Tổng số “Total Count”.
 
N missing

N missing là Số lượng giá trị còn thiếu trong mẫu. Số lượng giá trị bị thiếu đề cập đến các ô có chứa ký hiệu giá trị bị thiếu *. Minitab hiển thị giá trị này trong đầu ra là N *.
 

N nonmissing

N nonmissing là Số lượng giá trị không bị thiếu trong mẫu. Minitab hiển thị giá trị này trong đầu ra là N.

1. Trong mục Biến đầu vào “Input variable”, hãy nhập cột dữ liệu số để tính toán thống kê.

2. (Tùy chọn) Trong mục Lưu trữ kết quả tại “Store result in”, nhập một số không đổi (ví dụ: K1) hoặc tên hằng số. Nếu tên chứa khoảng trắng, hãy đặt tên trong dấu ngoặc kép.

TIP
Để xem một hằng số đã lưu, hãy chọn Data > Display Data.

1. Trong Biến đầu vào “Input variable”, hãy nhập một hoặc nhiều cột dữ liệu số để phân tích.

2. Trong Lưu trữ kết quả tại “Store result in”, hãy nhập số cột (ví dụ: C1) hoặc tên cột. Nếu tên chứa khoảng trắng, hãy đặt tên trong dấu ngoặc kép.

Sum

Tổng “Sum” là tổng của tất cả các giá trị dữ liệu. Tổng “Sum”  cũng được sử dụng trong các tính toán thống kê, chẳng hạn như giá trị trung bình “Mean” và độ lệch chuẩn “standard deviation”.


Mean

Giá trị trung bình “Mean” là giá trị trung bình của dữ liệu, là tổng của tất cả các quan sát “observation” chia cho số lượng quan sát “number of observation”.
 
Ví dụ: thời gian chờ (tính bằng phút) của năm khách hàng trong ngân hàng là: 3, 2, 4, 1 và 2. Thời gian chờ trung bình được tính như sau:



Như vây, trung bình một khách hàng chờ đợi 2,4 phút để được phục vụ tại ngân hàng.
 

Diễn giải

Sử dụng giá trị trung bình “Mean” để mô tả mẫu với một giá trị duy nhất đại diện cho trung tâm của dữ liệu. Nhiều phân tích thống kê sử dụng giá trị trung bình như một thước đo tiêu chuẩn cho trung tâm của sự phân phối dữ liệu.
 
Giá trị trung vị “Median” và giá trị trung bình “Mean” đều đo lường xu hướng trung tâm. Nhưng các giá trị bất thường, được gọi là giá trị ngoại lai, có thể ảnh hưởng đến giá trị trung vị “Median” ít hơn so với chúng ảnh hưởng đến giá trị trung bình “Mean”. Nếu dữ liệu của bạn là đối xứng, giá trị trung bình và giá trị trung vị là tương tự.


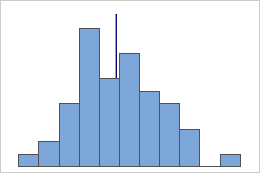Dữ liệu phân bố đối xứng (Symmetric)
 
 

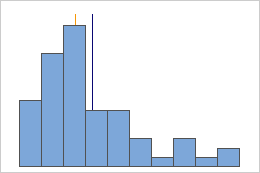Dữ liệu phân bố bất đối xứng (Not Symmetric)
 
Đối với phân phối đối xứng, giá trị trung bình “Mean” (đường màu xanh) và trung vị “Median” (đường màu cam) giống nhau đến mức bạn không thể dễ dàng nhìn thấy cả hai đường. Nhưng nếu dữ liệu phân bố không đối xứng, bạn sẽ nhìn thấy hai đường này này tách biệt.

 

StDev

Độ lệch chuẩn “StDev” là thước đo phổ biến nhất của độ phân tán, hoặc mức độ trải rộng của dữ liệu so với giá trị trung bình “Mean”. Ký hiệu σ (sigma) thường được sử dụng để biểu thị độ lệch chuẩn của một tập hợp “standard deviation of a population”, trong khi s được dùng để biểu thị độ lệch chuẩn của một mẫu “standard deviation of a sample”. Sự thay đổi ngẫu nhiên hoặc tự nhiên của một quá trình thường được gọi là nhiễu “Noise”.
 
Bởi vì độ lệch chuẩn có cùng đơn vị với dữ liệu, nó thường dễ hiểu hơn phương sai “variance”.
 

Diễn giải

Sử dụng độ lệch chuẩn để xác định mức độ trải rộng của dữ liệu so với giá trị trung bình. Giá trị độ lệch chuẩn cao hơn cho thấy mức độ lan truyền dữ liệu lớn hơn. Một nguyên tắc chung cho phân phối chuẩn “Normal distribution” là khoảng 68% giá trị nằm trong một độ lệch chuẩn của giá trị trung bình, 95% giá trị nằm trong hai độ lệch chuẩn và 99,7% giá trị nằm trong ba độ lệch chuẩn.
 
Độ lệch chuẩn cũng có thể được sử dụng để thiết lập một điểm chuẩn để ước tính sự thay đổi tổng thể của một quá trình.



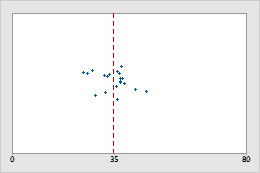Bệnh viện 1



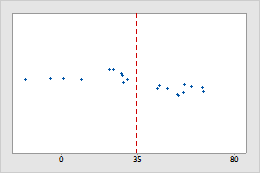Bệnh viện 2

 
Thời gian xuất viện

Quản trị viên theo dõi thời gian làm thủ tục xuất viện của các bệnh nhân đang điều trị tại khoa cấp cứu của hai bệnh viện. Mặc dù thời gian làm thủ tục xuất viện trung bình là như nhau (35 phút), nhưng độ lệch chuẩn là khác nhau đáng kể. Độ lệch chuẩn của bệnh viện 1 là khoảng 6 phút. Trung bình, thời gian xuất viện của một bệnh nhân lệch so với giá trị trung bình (đường nét đứt màu đỏ) khoảng 6 phút. Độ lệch chuẩn của bệnh viện 2 là khoảng 20 phút. Trung bình, thời gian xuất viện của một bệnh nhân lệch so với giá trị trung bình (đường nét đứt màu đỏ) khoảng 20 phút.
 

Minimum

Giá trị nhỏ nhất “Minimum” là giá trị dữ liệu nhỏ nhất.
 
Trong những dữ liệu này, giá trị nhỏ nhất là 7.
 

 

Diễn giải

Sử dụng giá trị nhỏ nhất “Minimum” để xác định lỗi ngoại lệ có thể xảy ra hoặc lỗi nhập dữ liệu. Một trong những cách đơn giản nhất để đánh giá mức độ lan truyền dữ liệu của bạn là so sánh giá trị nhỏ nhất “Minimum” và giá trị lớn nhất “Maximum”. Nếu giá trị nhỏ nhất rất thấp, ngay cả khi bạn xem xét trung tâm, độ lan truyền và hình dạng của dữ liệu, hãy điều tra nguyên nhân của giá trị cực trị “extreme value”.

Range

Phạm vi “Range” là sự khác biệt giữa giá trị dữ liệu lớn nhất “Maximum” và nhỏ nhất “Minimum” trong mẫu “Sample”. Phạm vi đại diện cho khoảng có chứa tất cả các giá trị dữ liệu.
 

Diễn giải
Sử dụng phạm vi “Range” để hiểu mức độ phân tán trong dữ liệu. Giá trị phạm vi lớn cho biết dữ liệu có độ phân tán lớn hơn. Giá trị phạm vi nhỏ chỉ ra rằng dữ liệu ít bị phân tán hơn. Bởi vì phạm vi được tính toán chỉ bằng cách sử dụng hai giá trị dữ liệu, nó hữu ích hơn khi xem xét với các tập dữ liệu nhỏ.

 

Median
Trung vị “Median” là điểm giữa của tập dữ liệu. Giá trị điểm giữa này là điểm mà tại đó một nửa số quan sát ở trên giá trị và một nửa số quan sát ở dưới giá trị. Trung vị được xác định bằng cách xếp hạng các quan sát và tìm quan sát ở số [N + 1] / 2 theo thứ tự được xếp hạng. Nếu số lượng quan sát là chẵn, thì trung vị là giá trị trung bình của các quan sát được xếp hạng ở các số N / 2 và [N / 2] + 1.
 

 
Đối với dữ liệu có thứ tự này, giá trị trung bình là 13. Nghĩa là, một nửa giá trị nhỏ hơn hoặc bằng 13 và một nửa giá trị lớn hơn hoặc bằng 13. Nếu bạn thêm một quan sát khác bằng 20, giá trị trung bình là 13,5, là giá trị trung bình giữa quan sát thứ 5 (13) và quan sát thứ 6 (14).
 

Diễn giải

Giá trị trung vị “Median” và giá trị trung bình “Mean” đều đo lường xu hướng trung tâm. Nhưng các giá trị bất thường, được gọi là giá trị ngoại lai, có thể ảnh hưởng đến Giá trị trung vị “Median” ít hơn chúng ảnh hưởng đến giá trị trung bình “Mean”. Nếu dữ liệu của bạn là đối xứng, giá trị trung bình và giá trị trung vị là tương tự.


Dữ liệu phân bố đối xứng


Dữ liệu phân bố không đối xứng
 
Đối với phân phối đối xứng, giá trị trung bình (đường màu xanh) và trung vị (đường màu cam) giống nhau đến mức bạn không thể dễ dàng nhìn thấy cả hai đường. Nhưng phân bố không đối xứng bị thì nó lệch sang phải.

 
 
Sum of Squares

Tổng bình phương “Sum of Squares” chưa hiệu chỉnh được tính bằng cách bình phương từng giá trị trong cột và tính tổng của các giá trị bình phương đó. Ví dụ: nếu cột chứa x1, x2, ..., xn, thì tổng bình phương sẽ tính (x₁² + x₂² + ... + x_n²). Không giống như tổng bình phương đã sửa “corrected sum of squares”, tổng bình phương chưa hiệu chỉnh bao gồm cả lỗi. Các giá trị dữ liệu được bình phương mà không trừ giá trị trung bình trước.
 
 
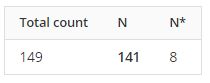
Total Count

Tổng số quan sát “Total count” trong cột. Dùng để biểu diễn tổng của Số quan sát bị thiếu “N missing” và Số quan sát hợp lệ “N nonmissing”.
 
Trong ví dụ này, có 141 quan sát hợp lệ và 8 giá trị bị thiếu. Tổng số quan sát “T count” là 149.


 
N

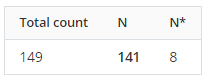
N là Số lượng giá trị quan sát hợp lệ trong mẫu.
 
Trong ví dụ này, có 141 quan sát hợp lệ được ghi lại.


 
N *

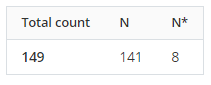
N * là Số lượng quan sát bị thiếu trong mẫu. Số lượng quan sát bị thiếu đề cập đến các ô chứa ký hiệu giá trị bị thiếu *.
 
Trong ví dụ này, 8 lỗi đã xảy ra trong quá trình thu thập dữ liệu và được ghi lại là các giá trị bị thiếu.

Nguồn: https://support.minitab.com/